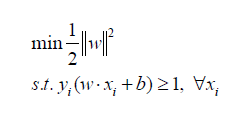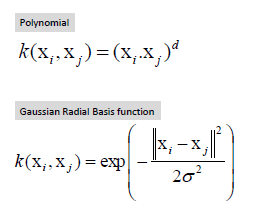| Map
> Data Science > Predicting the Future >
Modeling >
Classification > Support Vector Machine |
|
|
|
|
|
|
Support Vector
Machine - Classification (SVM)
|
|
|
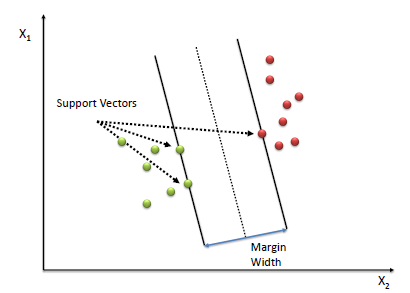
| A Support Vector Machine (SVM) performs classification by
finding the hyperplane that maximizes the margin between the two classes. The vectors
(cases) that define the hyperplane are the support vectors. |
|
|
|
|
|
|
| Algorithm |
|
|
- Define an optimal hyperplane: maximize margin
- Extend the above definition for non-linearly separable problems: have a penalty term for misclassifications.
- Map data to high dimensional space where it is easier to classify with linear decision surfaces: reformulate problem so that data is mapped implicitly to this space.
|
|
|
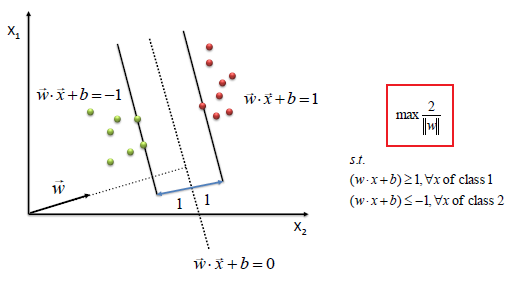
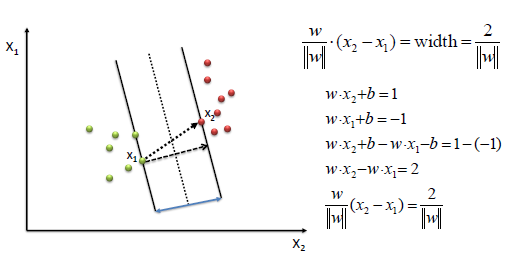
| To define an optimal hyperplane we need to maximize
the width of the margin (w). |
|
|
|
|
|
|
|
|
|
|
| We find w and b
by solving the following objective function using Quadratic Programming. |
|
|
|
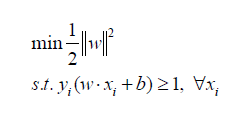
|
|
|
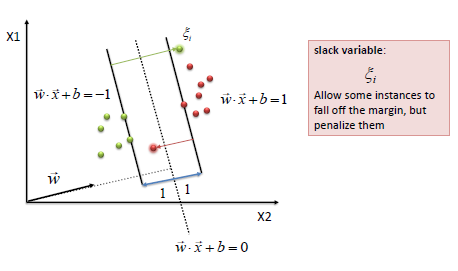
| The beauty of SVM is that if the data is linearly
separable, there is a unique global minimum value. An ideal SVM analysis should produce a hyperplane that completely separates the vectors
(cases) into two non-overlapping classes. However, perfect separation may not be possible, or it may result in a model with so many
cases that the model does not classify correctly. In this situation SVM finds the hyperplane that maximizes the margin and minimizes the
misclassifications. |
|
|
|
|
|
|
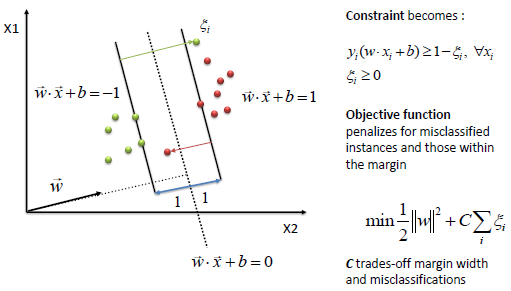
| The algorithm tries to maintain the slack variable
to zero while maximizing margin. However, it does not minimize the number
of misclassifications (NP-complete problem) but the sum of distances from
the margin hyperplanes. |
|
|
|
|
|
|
|
|
|
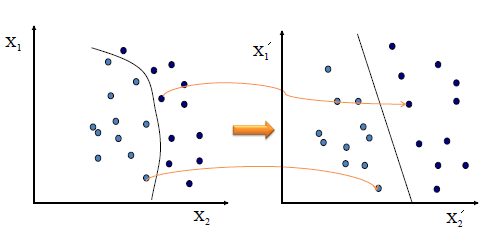
| The simplest way to separate two groups of data is with a straight
line (1 dimension), flat plane (2 dimensions) or an N-dimensional
hyperplane. However, there are situations where a nonlinear region can
separate the groups more efficiently. SVM handles this by using a kernel function
(nonlinear) to map the data into a different space where a hyperplane
(linear) cannot be used to do the separation. It means a non-linear function is learned by a linear learning machine in a
high-dimensional feature space while the capacity of the system is controlled by a parameter that does not depend on the dimensionality of the
space. This is called kernel trick
which means the kernel function transform the data into a higher dimensional
feature space to make it possible to perform the
linear separation. |
|
|
|
|
|
|
|
|
|
|
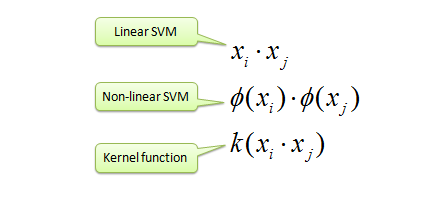
| Map data into new space, then take the inner
product of the new vectors. The image of the inner product of the data is
the inner product of the images of the data. Two kernel functions are
shown below. |
|
|
|
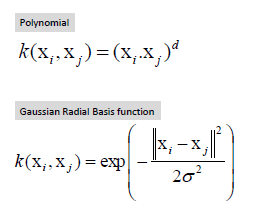
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|